An Integration of Adaptive Control Techniques with Portable Solar-Powered EV Charging with Particle Swarm Optimization (PSO)

Abstract

This paper presents a novel approach utilizing Particle Swarm Optimization (PSO) for enhancing the efficiency of solar-powered electric vehicle (EV) charging systems. With the increasing adoption of EVs and the imperative to transition towards renewable energy sources, optimizing the utilization of solar power for charging becomes crucial. The proposed system integrates photovoltaic (PV) panels to harness solar energy, providing a sustainable and renewable power source for EV charging. The key innovation lies in the application of PSO, a nature-inspired optimization algorithm, to dynamically adjust charging parameters based on real-time environmental conditions, grid electricity prices, and EV battery requirements. PSO offers a robust and efficient method for solving optimization problems by simulating the behavior of swarms in nature. In the context of solar-powered EV charging, the PSO algorithm iteratively adjusts charging rates and schedules to maximize solar energy utilization, minimize charging costs, and ensure optimal battery health. The integration of PSO optimization with solar-powered EV charging represents a promising step towards achieving sustainable and intelligent transportation solutions. Future research directions may include further optimization refinements, scalability studies, and real-world deployment to validate the practicality and effectiveness of the proposed approach in diverse environments and usage scenarios.

Introduction

I. INTRODUCTION

Electric Vehicles (EVs) have shown to be a viable alternative to hydrocarbon automobiles considering they emit no greenhouse gas and do not rely on crude oil-producing countries to determine gas prices. Other than this the entire full energy cycle is more efficient in the case of renewable energy, notably for solar photovoltaic (SPV) energy generation. We can readily observe how electricity rates remain reasonably stable while fuel costs surge throughout every international conflict. Considering all of these factors, electric vehicles are a better substitute to gasoline-powered vehicles. Whereas a significant amount of work is being undertaken to develop efficient electric vehicles and their corresponding infrastructural facilities, electric vehicles primarily use two charging schemes: on board charging and off-board charging. The charging circuit of the on-board is retained within the automobile itself, and it may be charged whether using AC or DC. The charging circuit is housed within the charging station in the case of the off board, and an EV may indeed be charged using either 1-phase AC, 3-phase AC, or DC power, each of which has advantages as well as disadvantages. Charging an EV using solar energy can be a difficult operation considering solar irradiance and temperature change over time, contrary to an idealistic situation where weather conditions and temperature are constant [1]. As a result, the power generated is indeed not uniform. Various conventional mathematical and neural computing-based optimization approaches and techniques are implemented to assess this and it is known as “Maximum power point tracking (MPPT) of solar arrays [2], and each MPPT algorithm setup has advantages as well as disadvantages. This is implemented in series with the circuit referred to as the DC-DC Buck/Boost converter, whereby the solar panel’s power output may very well be regulated by numerous MPP control methods mentioned above by altering the converter’s pulse width modulated (PWM) input signal. Using this, solar panels are maintained at their maximum power point (Vmp, Imp), going to charge the EV at the solar PV’s maximum power output [3]. Further to that, since solar photovoltaic systems can be broadly classified as grid connected or remote stand-alone systems, the system’s power capacity can differ widely from low-powered operation to high-powered operation, the median generation capacity can differ of these systems is still well above hundreds of kW (kilo-Watts). It is also known that a sizable SPV can produce hundreds of amps of direct current, which also, if connected directly into the Electric vehicle, can cause damage [4]. In literature, different solutions for PV-powered EV chargers are proposed, such as Multifunctional Off-Board EV Charger [5], Bidirectional EV Charger [6], Z-Source based charger [7], Wireless EV Charger [8], Intermittency mitigated EV Charger [9], etc.

All these chargers are absolutely fine and suitable for EVs. However, in all these configurations and topologies, the grid is mandatory with PV to operate during the charging process. In the case of the standalone condition, these techniques will not work. Therefore, this paper proposes a novel topology and control to operate in a standalone condition Additionally, an EV has a charging current rating that ordinarily ranges from 10% to 15% of the maximum capacity of the EV battery, with most EVs receiving up to 32A for power delivery up to 7.4KWs from a typical charger, where the EV’s battery is not continuously cooled throughout this charging period. Consequently, current must be monitored before being supplied into the EV [10], which may be performed by analyzing the solar array’s output with sensors [11], [12]. Therefore, although solar PV can be found in even the most sparsely populated areas due to the increased intervention from the government, EV chargers are currently difficult to discover even those in tier 2 or 3 cities, let alone in villages or isolated areas. And hardly any research has been dedicated to the accessibility of charging infrastructure in remote locations where, if an EV user becomes stuck, they would have been unable to use an EV charging station since incorporating complex and costly charging stations for electric may not even be very economical in areas where the number of consumers is rather relatively small, as well as remote locations make it much more difficult for repair or replacement, which arises as a potential hazard which will always be considered as part.

These characteristics summarize the fact that this is not the real solution to this particular circumstance. Therefore, in big countries like the USA, Canada, China, Russia, India, Australia, as well as in a few Arabian countries, governments are planning to provide pillar top solar panels in the remote locations for EV charging in an emergency situation (such as shown in Fig. 1). To operate in this situation, a special charging adapter requires, which extracts maximum power from the panel using MPPT technique and monitors charging current and safely completes the charging process. Therefore, as conclusion, can see the need for a compact, cost-effective charging solution that can be immediately linked to any Photovoltaic system and stored within the car and utilized in cases, for example like these as well as routine everyday charging needs and requirements. Even if certain work is underway in this area as well, wherein multiple sensors are being used to control the power fed into the Electric vehicle based on the capacity of the battery [13], [14], it uses a large number of sensor nodes, making it bulky and expensive, as well as increasing the possibility of electro-magnetic interference in the system. Furthermore, there is unquestionably no system on the market that can accomplish these two objectives, namely effective MPPT operating of solar photovoltaic and current strictly controlled charging of EV.

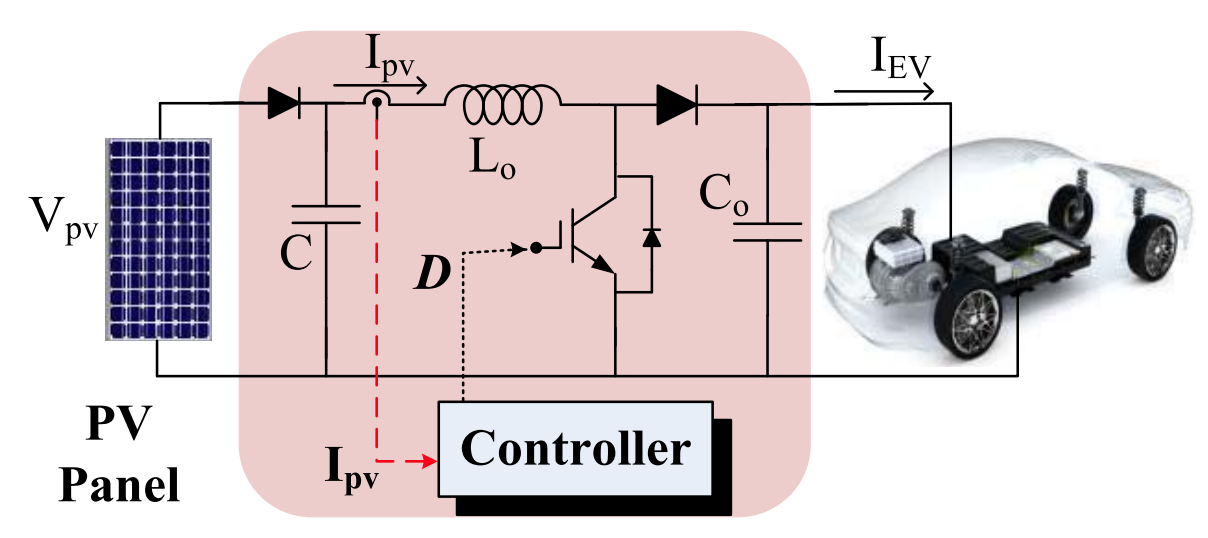FIGURE 1. Single sensor-based circuit of EV charging adapter

A. Description of Components:

Solar Photovoltaic: This component represents the photovoltaic (PV) panels that harness solar energy and convert it into electrical energy.

Solar Energy: The electrical energy generated by the solar panels.

Particle Swarm Optimization (PSO): PSO algorithm is applied to optimize the charging strategy based on real-time environmental conditions, grid electricity prices, and EV battery requirements.

Charging Strategy: The optimized charging strategy generated by the PSO algorithm, which determines the charging rates and schedules for the electric vehicle.

Electric Vehicle: Represents the electric vehicle being charged using solar power.

B. Standard PSO Algorithm

The particle swarm optimisation (PSO) algorithm was first introduced by Kennedy and Eberhart in 1995. The method is based on the natural process of the school of fish or the flock birds follow when they are searching for food. When birds are flying and searching randomly for food, birds in the flock share their discovery and help the entire flock achieve the best hunt, which results in increased search efficiency. PSO is an optimisation algorithm that offers a population-based search method in which individual particles utilise the information supplied by other particles to adjust their positions over time based on their own experiences as well as the experiences of other particles. Finding a function’s maximum or minimum on a multidimensional vector space is the ideal application for PSO.

II. PROPOSED CONCEPT

A. PV CONVERSION CHAIN

The PV conversion chain illustrates in figure, MPP is reached through controlling the DC-DC converter with a system using a MPPT controller. The strategy of the MPPT controller allows to optimize the transfer of power from the PV panel to the load.

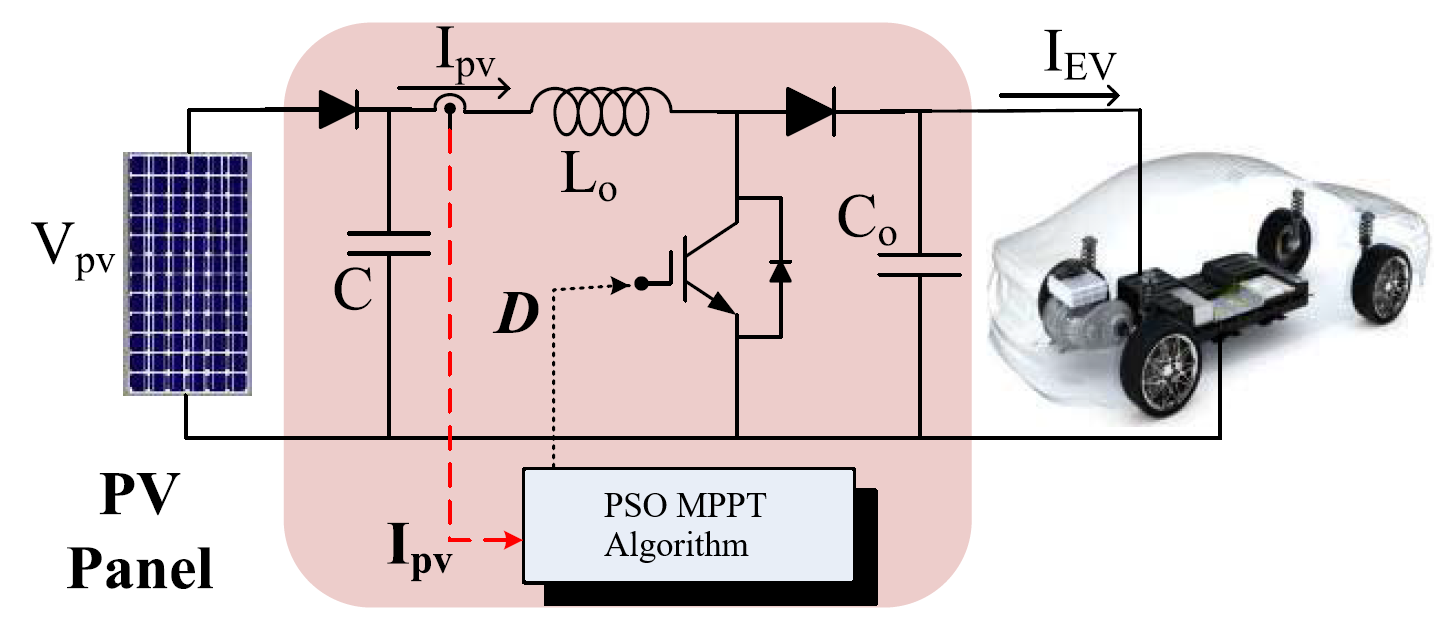Fig 2. Elementary chain of photovoltaic conversion.

The simulation of a system in the figure of renewable energy in general, and solar system “photovoltaic” in particular the optimizing system adapted by DC-DC converters static. Then the influence of temperature and irradiance on the optimal parameters (Power of MPP, VMPP) of a solar system is analysed in a way to operate a PV generator at its maximum power. This system includes a photovoltaic generator, “Boost & Buck”, converter and a load. Model and simulation system (solar panel, DC-DC converter command and load) is obtained through Matlab-Simulink software.

III. PV PANEL MODEL

In order to model our PV panel, we start with a simple model which is one of a PV elementary cell. The configuration that below figure presents is the most common equivalent schema of a solar cell. It is composed of a source of variable current Ipv, connected in parallel with a diode D, characterizing the junction of semi-conductors which make the solar cell, and a parallel resistance Rp. To this assembly, another resistance Rs is added in series. In model of a PVG issues is defined by the following equations:

Fig3.  Equivalent electric circuit of solar cell

• I0: Diode reverse saturation current (A).
• Ipv,n: Current measured under Standard Test Conditions (A).
• I, V: PVG current (A) and voltage (V).
• Isc and Voc: Short circuit current (A) and Open circuit voltage (V) measured under Standard Test Conditions.
• Rs, Rp: Series resistance (=0.2365 Ω) and parallel resistance (=415.405 Ω) respectively

A. Static Converter Type Buck

In our research, the suggested system contains a power converter DC-DC type Buck, driven by using the Pulse Width Modulation principle. This converter is model by the equivalent electric schema in below figure.

As far as the simulations of the studied converter are concerned, the parameters we have used are: the resistance of the load being Rc = 3 Ω, the capacitance of the capacitor being C = 4.7 μF, the inductance of the inductor being L = 2 mH, D being freewheeling diode and T being a transistor type MOSFET. During the operation in continuous mode of this buck converter, the average values of the output voltage Vs and input voltage Ve are proportional as follows:

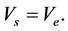
The proportionality coefficient α, being the duty cycle of values ranging from 0 to 1. In this present case, we use an average model of a buck converter, that is, VD ≈ αVe. Therefore, this converter will be described by the following equations:

To limit the ripples of the current and voltage at the level of the load, the LC cell,

Fig4. Equivalent electric circuit of buck converter

 constitutes a low-pass filter. To size this filter, we determine the minimal values of the inductance L and the capacitance C, bearing in mind the following constraints, studied by a number of authors:

• The current through the inductor must be in a reasonable range in all load conditions as the converter operates in continuous mode.
• The maximum output voltage ripple must not exceed 5% of the output voltage Vs.

Considering these constraints, the low-pass filter LC must respond to all the conditions of the following relations, where fc corresponds to the PWM switching frequency:

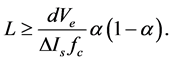
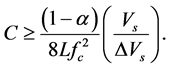
IV. MPPT TRACKING CONTROLLERS

The power chain supplies a DC load by the PVG through a static converter (SC) driven by a MPPT controller and based on one of the algorithms “Fuzzy TS”, “P&O” or “PSO”. The MPPT controller adjusts the duty cycle of the SC in such a way that the power provided by the PVG is maximum at its boundaries.

Fig5 PV system with buck converter driven by MPPT

Although solar energy is available throughout the day its insolation varies from morning to evening and with changing climatic conditions. As the efficiency of solar PV panel is low it becomes mandatory to extract maximum power from the PV panel at any given period of time. Several maximum power point tracking (MPPT) techniques are proposed for the purpose. Incremental conductance MPPT technique has higher steady-state accuracy and environmental adaptability. This paper investigates implementation issues of Incremental conductance MPPT algorithm. High frequency DC-DC Buck converter is used to interface PV panel with load. The Matlab Simulink model of the system is developed and results are validated with experimental results obtained using laboratory prototype of the system.

V. PSO CONTROLLER “PARTICLE SWARM OPTIMISATION”

1. The basic PSO algorithm technique is a robust stochastic optimization technique based on the movement and intelligence of swarms. It applies the concept of social interaction to problem solving. It uses a number of agents (particles) that constitute a swarm moving around in the search space looking for the best solution.

Each particle keeps track of its coordinates in the solution space which are associated with the best solution (fitness) that has achieved so far by that particle. This value is called personal best, P best.

Another best value that is tracked by the PSO is the best value obtained so far by any particle in the neighbourhood of that particle. This value is called G best.

During the optimization process, the particles take up the objective function’s values, while their G best and P best are saved. The basic PSO algorithm which determines the next velocity and position of the candidate solution can be given mathematically as:

In the afore mentioned expression, i represents the variable of the optimization vector, k is the number of iterations, and  respectively the velocity and position of the ith variable within k iterations, the parameter w is known as inertia that maintains a balance between the local and global search. c1 and c2 are acceleration constants. r1 and r2 are two generated random numbers which are uniformly distributed in the interval [−1, 1].

The variable Pbesti records the best position affected by the ith particle up to the exact time of measurement. The following equation indicates that this position is only recorded as Pbesti if the condition stated below is satisfied.

2. Configuration of PSO parameters

The search space of the problem in which each position represents an Output Voltage value as a solution to the MPPT problem. The evaluation of the particles is based on the Output Power of the PV panel respective to the final voltage value which is indicated by fit as the fitness evaluator for the particles. The following equation shows the position matrix of the n particles which represents n solutions to the MPPT problem.

where  is the position of Ith particle at kth iteration.

Therefore, the algorithm must be initialized when the following equation is satisfied.

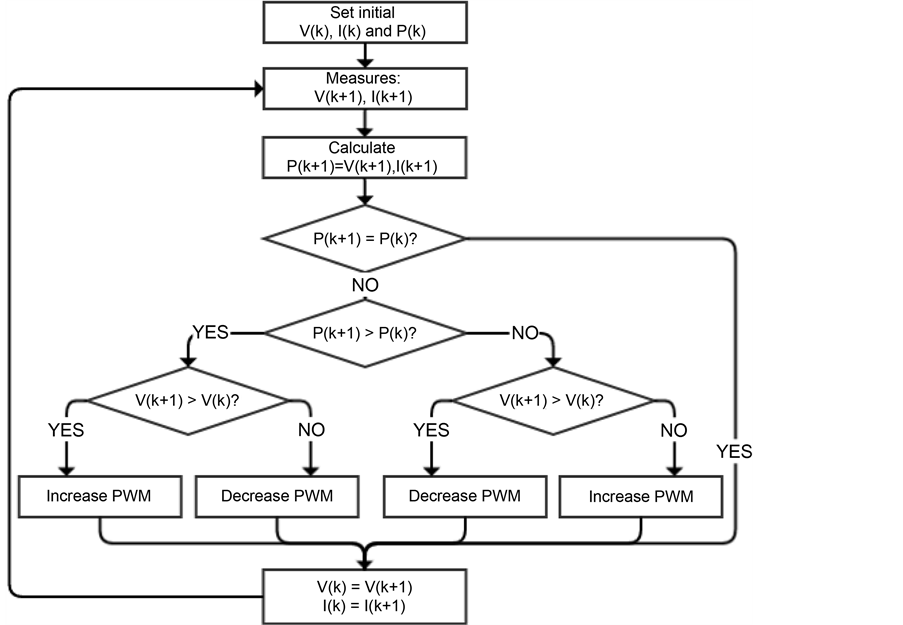
Fig 6. Flow chart of PSO algorithm

The PSO algorithm implementation process in this paper is as follow:

• Initialize the size of swarm, dimension of search space, maximum number of iterations, and the PSO constants w, c1 and c2. Define the random numbers r1 and r2.
• Find out the current fitness of each particle in the population.
• Attribute the particles with random initial positions and velocities.
• Evaluate fitness value of each particle.
• Calculate the global best fitness value: current global best fitness = min (local best fitness).
• Update the particle velocity and position for next iteration. Find out the current fitness of each particle: If current fitness < local best fitness, set local best fitness = current fitness.
• Determinate the current global best fitness (current global best fitness = min (local best fitness)): If current global best fitness < global best fitness, then global best fitness = current global best fitness. The position corresponding to global best fitness is assigned to Gbest.
• Repeat Steps 6 and 7 until achieved the maximum number of iterations or there is no improvement of the global best fitness value.
• Terminate the iterative algorithm when the criterion is reach

VI. RESULTS

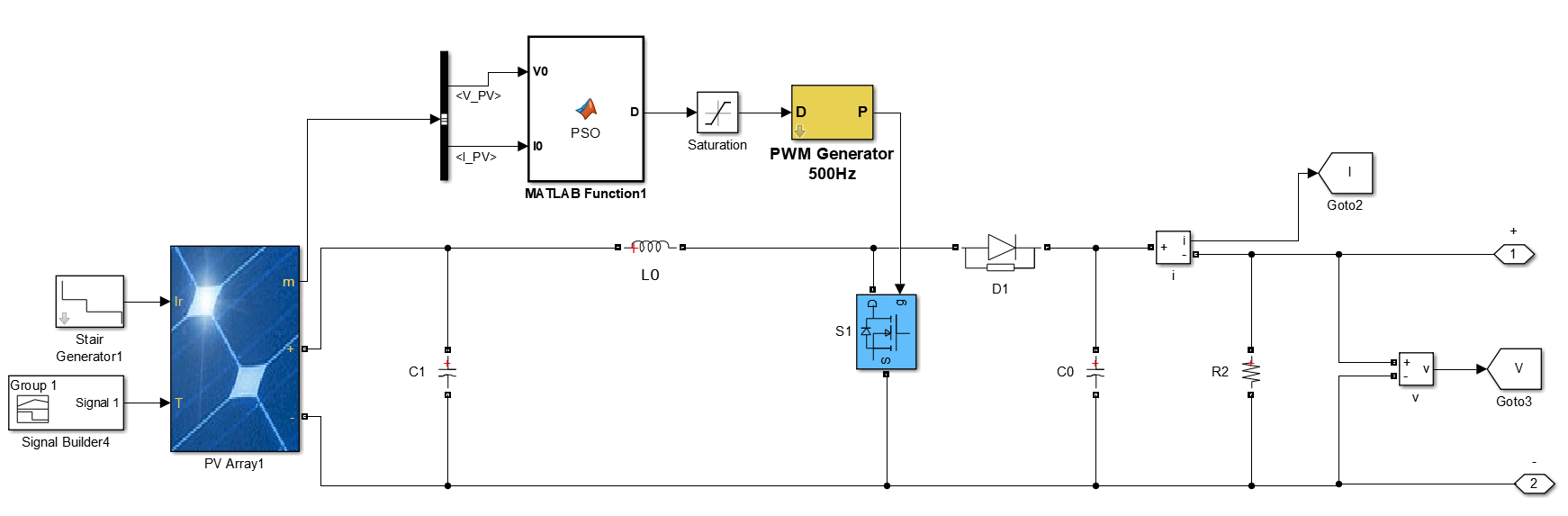Fig7. Solar PV array with the Proposed MPPT boost converter

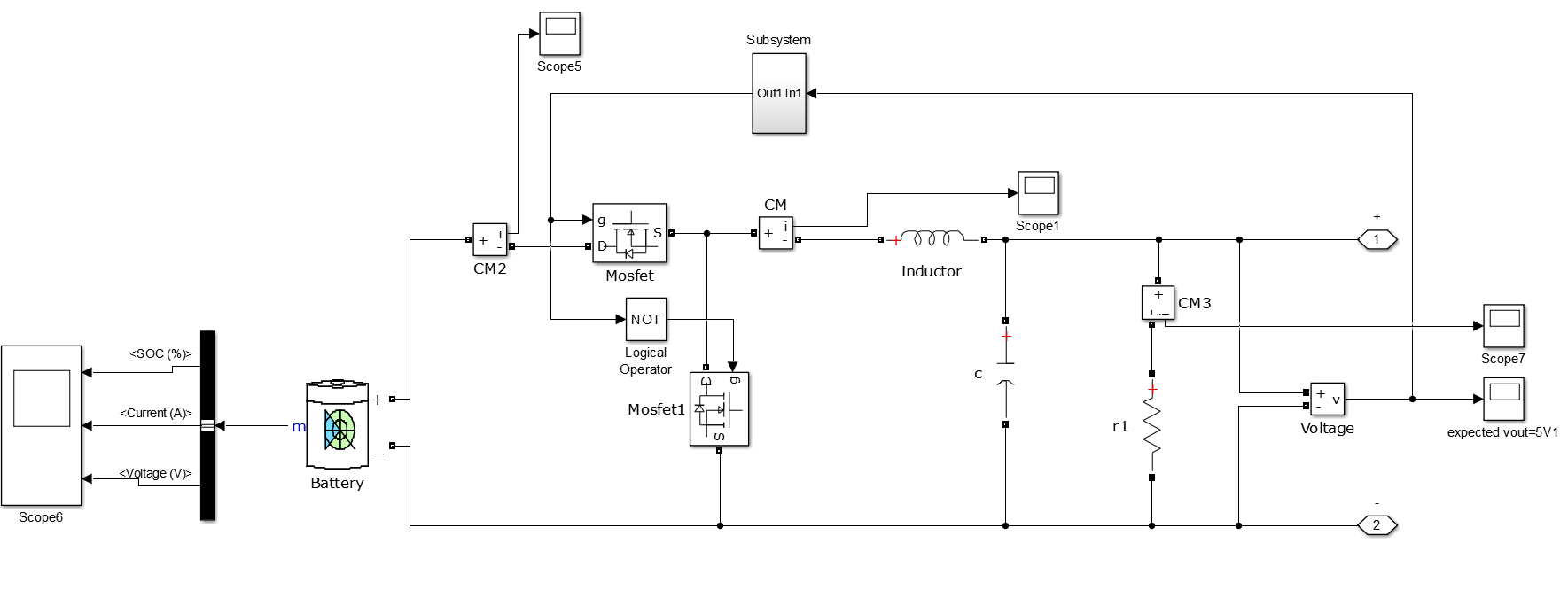Fig8. Battery pack with the bidirectional boost converter

A. CASE-1: SOLAR IRRADIANCE VARIATION IN STEP MANNER

In case-1, solar irradiance has been varied in a stepwise manner as shown in Fig. 9 for a period of 5 secs, i.e., from 0.5 secs to 5.5 secs varies from initially 1000W/m2 to 500W/m2 to 900W/m2 to 600W/m2 to 800W/m2 and finally to 700W/m2 while the change in solar irradiance is in the stepped manner.

Here, output waveforms of solar PV are shown in Fig. 10, where Fig. 10 is for PSO [12], In Fig. 10, it can be seen that in the steady-state condition, the significantly high number of fluctuations are in PV voltage (VPV), PV current (IPV) and PV power (PPV)

This is happening because of the oscillating duty cycle generated by PSO. The waveforms of the duty cycle obtained by the PSO algorithm are also shown in Fig. 10(a) and Fig. 10, respectively.

Moreover, during dynamic change conditions, the time taken to transition from one mode of operation to another taking more time in the case of PSO [12] due to the rigid and constant nature of step size. While comparing Fig. 10 which is PSO respectively, with Fig. 10 that is our proposed method PSO, these unwanted fluctuations are removed significantly in steady state conditions, in dynamic change conditions, transition time is much faster which can be noticed between 0.5s to 2.5s. Moreover, in steady-state conditions, this fluctuation becomes completely negligible.

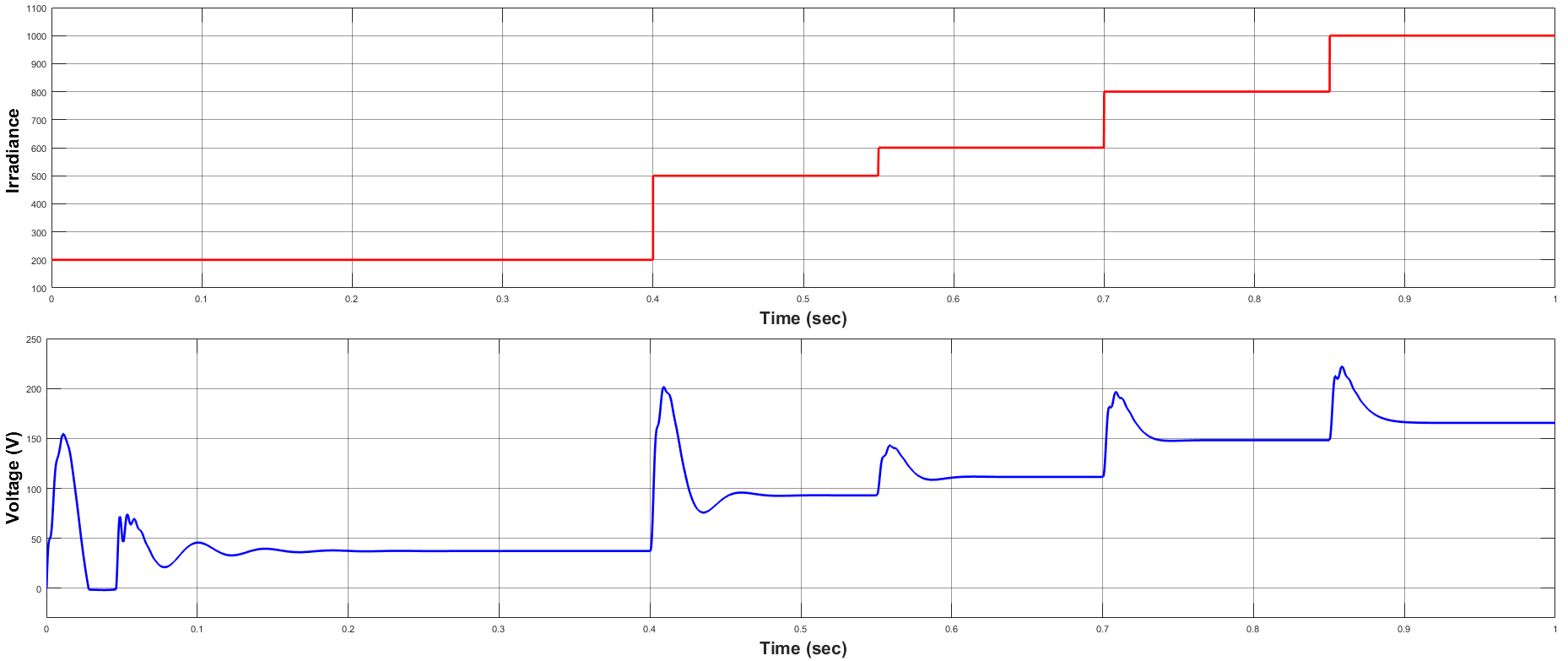FIGURE 10. The obtained waveforms of solar panel in case-1 test condition by using PSO

B. CASE-2: SOLAR IRRADIANCE VARIATION IN RAMP MANNER

In case-2, solar irradiance has been varied in ramp wise manner as shown in Fig. 12 for a time period of 5s, i.e., from 0.5s to 5.5s and varies from initially 1000W/m2 to 400W/m2 to 900W/m2 to 500W/m2 to 800W/m2 and finally to 700W/m2 while the change in solar irradiance is in a ramp manner. In this condition, the obtained output waveforms of solar PV are shown in Fig. 13, where Fig. 11 is for PSO, it can be clearly seen that in steady-state condition, significantly huge fluctuations are in VPV, IPV and PPV. This is happening because of the oscillating duty cycle generated by PSO. The waveforms of D obtained by PSO algorithm are also shown in Fig. 11, respectively. Moreover, during dynamic change condition, during shifting from one mode of operation to another, deviation on the tracking track is, in the case of PSO, because of their rigid and constant nature of step size. It is following the change with the slop of ramp. Moreover, during tracking, the fluctuation and deviations are completely negligible.

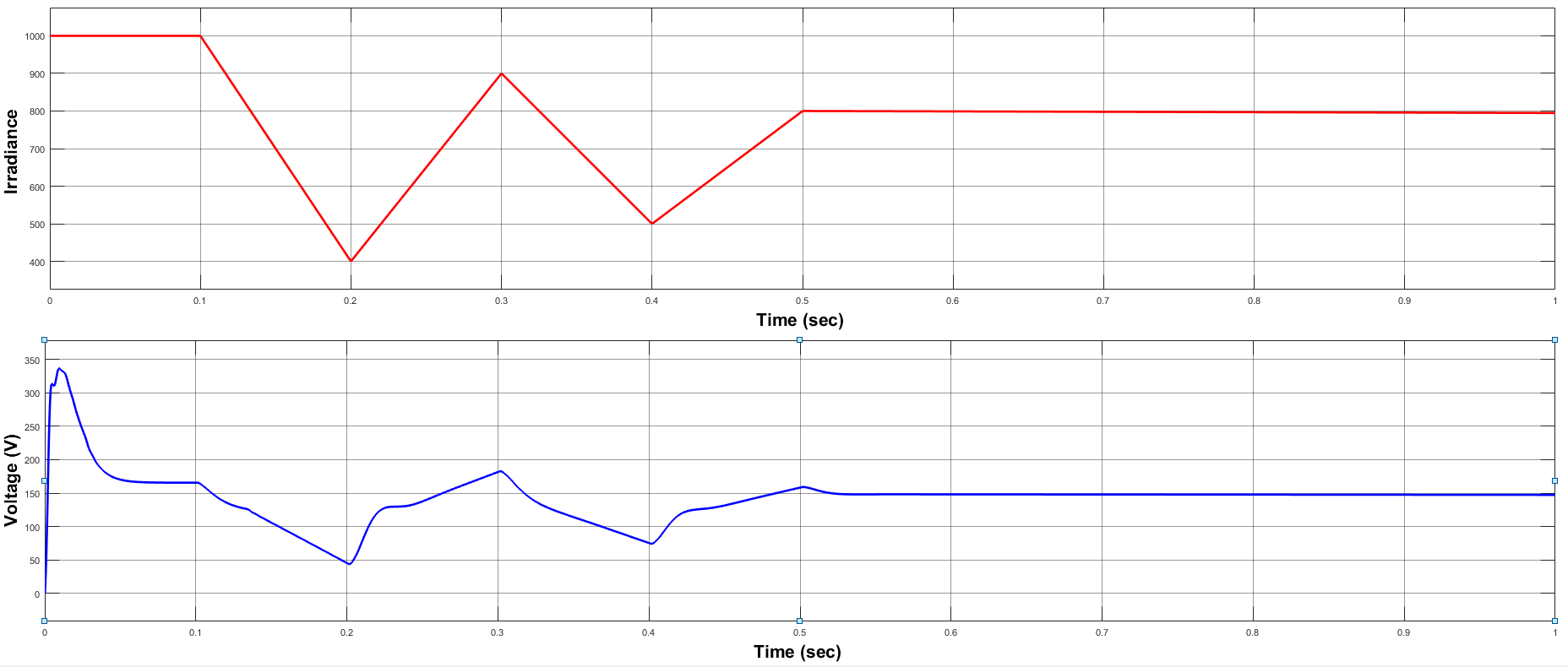FIGURE 11. Solar irradiance pattern with ramp change and the output Voltage

The waveforms of EV battery charging are shown in Fig. 11, depict the performance of PSO [12] algorithm. The oscillations in the steady-state condition is negligible, and in the dynamic change condition, deviation on the tracking track is also negligible, which enhances the charging process and efficiency of the system

Conclusion

In this paper, a novel charging adapter topology has been proposed, which is based on a single current sensor. Low cost, fast response and high sensitivity to dynamic change, these behaviours of the current sensor make it an accurate and economical charger. Moreover, a PSO algorithm has been proposed to accomplish MPPT operation and battery charging management. PSO algorithm has very good condition estimation and decision-making capability, which performs MPPT very accurately, monitors the charging process, and keeps it safe in adverse conditions. The capability of developed charging adapter with PSO algorithm has been evaluated on Hardware prototype, as well as comparative studies have been performed w.r.t. state-of the-art techniques, where developed charging scheme shows the dominancy over other techniques. The only limitation of this technique is required comparatively slightly bigger processer to execute this control logics.

References

[1] Mataifa, H.; Krishnamurthy, S.; Kriger, C. Volt/VAR Optimization: A Survey of Classical and Heuristic Optimization Methods. IEEE Access 2022, 10, 13379–13399. [Google Scholar] [CrossRef] [2] Dagal, I.; Akin, B.; Akboy, E. A novel hybrid series salp particle Swarm optimization (SSPSO) for standalone battery charging applications. Ain Shams Eng. J. 2022, 13, 101747. [Google Scholar] [CrossRef] [3] Roy, A.; Olivier, J.; Auger, F.; Auvity, B.; Schaeffer, E.; Bourguet, S.; Schiebel, J.; Perret, J. A combined optimization of the sizing and the energy management of an industrial multi-energy microgrid: Application to a harbour area. Energy Convers. Manag. X 2021, 12, 100107. [Google Scholar] [CrossRef] [4] Zhang, X.; Son, Y.; Cheong, T.; Choi, S. Affine-arithmetic-based microgrid interval optimization considering uncertainty and battery energy storage system degradation. Energy 2022, 242, 123015. [Google Scholar] [CrossRef] [5] Madathil, S.C.; Nagarajan, H.; Bent, R.; Mason, S.; Eksioglu, S.; Lu, M. Algorithms for Optimal Topology Design, Placement, Sizing and Operation of Distributed Energy Resources in Resilient Off-grid Microgrids. arXiv 2018, arxiv.1806.02298. [Google Scholar] [6] Li, S.; Zhu, J.; Dong, H.; Zhu, H. A novel rolling optimization strategy considering grid-connected power fluctuations smoothing for renewable energy microgrids. Appl. Energy 2022, 309, 118441. [Google Scholar] [CrossRef] [7] Zhang, X.; Wang, Z.; Lu, Z. Multi-objective load dispatch for microgrid with electric vehicles using modified gravitational search and particle swarm optimization algorithm. Appl. Energy 2022, 306, 118018. [Google Scholar] [CrossRef] [8] Gomes, I.; Melicio, R.; Mendes, V. A novel microgrid support management system based on stochastic mixed-integer linear programming. Energy 2021, 223, 120030. [Google Scholar] [CrossRef] [9] Zia, M.F.; Elbouchikhi, E.; Benbouzid, M. Optimal operational planning of scalable DC microgrid with demand response, islanding, and battery degradation cost considerations. Appl. Energy 2019, 237, 695–707. [Google Scholar] [CrossRef] [10] Habib, H.; Wang, S.; Elkadeem, M.; Elmorshedy, M. Design Optimization and Model Predictive Control of a Standalone Hybrid Renewable Energy System: A Case Study on a Small Residential Load in Pakistan. IEEE Access 2019, 7, 117369–117390. [Google Scholar] [CrossRef] [11] Soykan, G.; Er, G.; Canakoglu, E. Optimal sizing of an isolated microgrid with electric vehicles using stochastic programming. Sustain. Energy Grids Netw. 2022, 32, 100850. [Google Scholar] [CrossRef] [12] Budiman, F.N.; Ramli, M.A.; Bouchekara, H.R. Optimal scheduling of a microgrid with power quality constraints based on demand side management under grid-connected and islanding operations. Int. J. Electr. Power Energy Syst. 2023, 155, 109650. [Google Scholar] [CrossRef] [13] Tran, H.G.; Ton-That, L.; Thao, N.G.M. Lagrange Multiplier-Based Optimization for Hybrid Energy Management System with Renewable Energy Sources and Electric Vehicles. Electronics 2023, 12, 4513. [Google Scholar] [CrossRef] [14] Kweon, J.; Jing, H.; Li, Y.; Monga, V. Small-signal stability enhancement of islanded microgrids via domain-enriched optimization. Appl. Energy 2023, 353, 122172. [Google Scholar] [CrossRef] [15] Majeed, M.A.; Phichisawat, S.; Asghar, F.; Hussan, U. Optimal Energy Management System for Grid-Tied Microgrid: An Improved Adaptive Genetic Algorithm. IEEE Access 2023, 11, 117351–117361. [Google Scholar] [CrossRef]

Copyright

Copyright © 2024 Kanimoni Hareesh, Dr. M. Saravanan. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.